Vibration sensing with the optical fibre Mach-Zehnder interferometer

1. Institute of Technical Physics, Military University of Technology, ul. Gen. Sylwestra Kaliskiego 2, 00-908 Warsaw, Poland

Abstract

Vibration is a ubiquitous phenomenon that occurs in everyday life and people are exposed to it almost all the time. Most often, vibration is measured using electromechanical devices such as piezoelectric, piezoresistive, or capacitive accelerometers. However, attention should be paid to the limitations of such vibration sensors. They cannot operate in the presence of strong electromagnetic fields. Measurements with electromechanical devices require physical contact between the sensor and the vibrating object, which is not always possible due to the design of the sensor and device. The possibility of a non-contact vibration measurement in harsh environments is provided by the technology of interferometric fibre optic sensors. This paper reports the principle of operation, design aspects, experimentation, and performance of a Mach-Zehnder interferometric setup for the measurement of vibration frequency. There are different sensing arms implemented in the interferometer: single-mode, polarization-maintaining, and tapered optical fibre. The paper emphasises the simplicity of the set-up structure and the detection capabilities based on the interferometric sensing giving the possibility of constructing a commercial vibration sensor for all industry demands.

Introduction

Vibration is mostly generated by mechanical disturbances that can be caused, for example, by sound, noise, engine, or wind. The technology of monitoring and analysing this phenomenon is of great importance in scientific research and engineering applications. Accurate and precise continuous vibration measurement is essential for detecting anomalies and providing early warning of infrastructure damage. Vibration level detection is very important, for example, in monitoring the operation of machines [1], the condition of building structures [2, 3] and forecasting natural disasters [4, 5]. Vibrations can be transferred to the human body and belong to the group of harmful factors. For this reason, vibration measurements at workplaces, wherever a person may be exposed to them, are extremely important. Most often, vibration is measured using electromechanical devices such as piezoelectric, piezoresistive, or capacitive accelerometers [6].

The energy of mechanical vibrations is converted by an accelerometer into an electrical signal, which is then converted into a measurement result. This phenomenon results from the deformation of a structure, which creates an electric charge on the surface. Nevertheless, special environmental conditions, such as a strong electromagnetic field, limit the use of such vibration sensors. Such a field adversely affects the correct operation of traditional sensors, making them difficult to operate or completely useless in some cases. Measurements with electromechanical devices require physical contact between the sensor and the vibrating object, which is not always possible due to the design of the sensor and the measured object [7]. The above, combined with high maintenance costs, means that classic vibration sensors do not meet the real needs of modern technical measurements [8–10]. The possibility of a non-contact vibration measurement is provided by the technology of interferometric fibre optic sensors.

Fibre optic technology is one of the most dynamically developing fields of science [11, 12]. Optical fibre sensors are used in many industrial processes, diagnostics or devices monitoring, wherever knowledge about the dis-placement, pressure, temperature, flow rate, or chemical composition of substances is necessary [13, 14]. They provide very high sensitivity and application versatility. In addition, optical fibres, thanks to their dielectric and material properties, allow these devices to operate in the presence of electromagnetic fields, aggressive environ-ments, or high voltage. The principle of operation is based on modulation of one of the parameters of the light wave propagating in the optical fibre by the measured physical quantity. Three basic elements can be distinguished in the interferometric fibre optic sensor: a light source, an inter-ferometer, and an electronic signal detection system [15]. Recently, optical fibre vibration sensors mostly include point [16–19], quasi-distributed [20], and distributed sensors [21, 22]. Several schemes of the point sensors including fibre Bragg grating (FBG), Fabry-Pérot inter-ferometer (FPI) [23, 24], self-mixing [25], and Doppler vibrometer [26, 27] are used for vibration sensing. The quasi-distributed fibre optic sensors are mostly based on the FBG, FPI, and fibre surface plasmon sensors. The FBG technology offers many possibilities such as the construc-tion of a low-cost accelerometer system capable of detecting frequencies up to 45 Hz [28] or an FBG accelerometer based on a diaphragm offering a response range from 10 to 200 Hz [29]. In 2012, Guo et al. reported an extrinsic FP interferometric (EFPI) optical sensor based on an ultra-thin silver film for ultrasonic detection [30].

Whereas Wang et al. presented an infra-sound sensor based on a polymer diaphragm in 2016 [31]. Nevertheless, the above-mentioned technologies demand early knowledge of the potential vibration point. The recent available distrib-uted optical fibre vibration sensors enable a continuous, real-time vibration monitoring over distances from a few meters to tens of hundreds of kilometres. In comparison to quasi-distributed sensing techniques, distributed fibre sensors have the advantage of providing information along the entire length of the fibre at every point. Therefore, external vibrations can be detected and located from anywhere without any contact with sensors. Distributed optical fibre sensing technology provides high sensitivity, large dynamic range, immunity to electro-magnetic interference, and simple structure [32–35]. They are capable of establishing an autonomous, continuous monitoring of vibration in harsh environments together with desirable shape and size. They are mainly based on the interfero-metric and backscattering technology. Most attention has been paid to the Sagnac interferometer [36], Mach-Zehnder interferometer (MZI) [37, 38], and Michelson interferometer (MI) [39]. The backscattering sensors mainly use optical frequency domain reflectometer (OFDR) and optical time domain reflectometer (OTDR). Recently, the combination of an interferometer and OTDR has been more and more popular, such as the use of an MZI and the phase-sensitive optical time domain reflectometer (Φ-OTDR) where a spatial resolution of 5 m and a frequency response of 6.3 MHz have been obtained under a 1150 m sensing optical fibre [40].

This paper presents the optical fibre Mach-Zehnder configuration for vibration detection. Three different sensing arms have been applied to obtain the wide frequency band of the sensor: standard single-mode optical fibre (SMF-28), single-mode polarization-maintaining (PM) fibre, and single-mode tapered optical fibre (TOF). The conducted experiments revealed that the constructed optical fibre MZI detected signals of different frequencies in the range from 1 Hz to 10 kHz.

Theory of the MZI

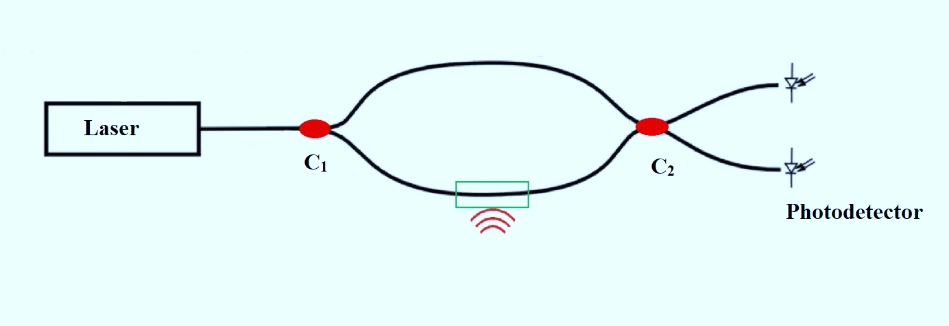
An optical fibre MZI (Fig. 1) contains a light source that emits coherent radiation propagated to the SMF. The generated wave is split equally by a 1 × 2 or 2 × 2 optical fibre coupler C1. Those two light waves propagate in two arms of the interferometer, named sensing and reference arm, respectively. The second optical fibre coupler C2, a 2 × 2 type is the point where the interference phenomenon takes place. The interference result is registered by the photodetectors. The measured quantity affects the inter-ferometer sensing arm, changing the interference image which, in turn, carries information about the detected quantity value.

Assuming that the polarization state of the beams propagated in optical fibres remains unchanged, the path of light coherence is much larger than the difference in the length of the interferometer optical paths, and the system has no losses, the electric field at photodetectors 1 and 2 can be written as [41, 42]

\( E_1=E_0 k_{11} k_{21} \exp \left(j \phi_{\mathrm{S}}\right)+E_0 k_{12} k_{22}\left(j \phi_R\right) \) (1)

\( E_2=E_0 k_{11} k_{22} \exp \left(j \phi_{\mathrm{S}}\right)+E_0 k_{12} k_{21}\left(j \phi_{\mathrm{R}}\right) \) (2)

where: k_nm (m, n = 1 or 2) – the coupling coefficient of the m- and n-th coupler arm, E₀ – the electric field amplitude of the light source, ϕS and ϕR – the phases of the sensing and reference beam, respectively, determined by the relations

\( \phi_{\mathrm{S}}=n_{\mathrm{S}} k l_{\mathrm{S}} \) (3)

\( \phi_{\mathrm{R}}=n_{\mathrm{R}} k l_{\mathrm{R}} \) (4)

where: n_S, n_R, l_S, l_R – the effective refractive index and the fibre length of the sensing (S) and the reference (R) arm, k – the wavelength number.

The coupling coefficients k_nm are the complex numbers and in the case of an ideal 2 × 2 coupler, the coupled beam experiences an additional phase delay of π/2. Therefore, assuming kn1 as a real number, one obtains kn2 as the imaginary number kn2 = jkn1.

By introducing the notation Δ = S − R and assuming the use of ideal 3 dB symmetric 2 × 2 couplers (k₁₁ = k₁₂ = k₂₁ = k₂₂ = 1/2), the intensity at the photo-detector 1 and 2 can be written as follows:

\( I_1=\frac{I_0}{2}[1-\cos \Delta \phi] \) (5)

\( I_2=\frac{I_0}{2}[1+\cos \Delta \phi] \) (6)

When the sensing arm experiences an external vibration and the reference arm is shielded from changes in the external vibration, changes in the length and refractive index cause phase modulations between the sensing and reference arms. The phase modulations are converted into the intensity modulation in the coupler C2 and recorded by the photodetector.

Experimental set-up

In order to detect vibration signals with a given frequency, a special experimental set-up has been performed, which schema is presented in Fig. 2.

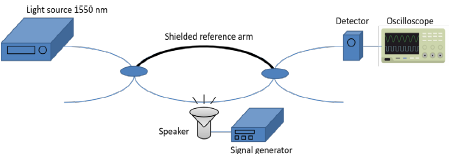
The set-up contains two 2 × 2 optical fibre couplers with a 50:50 power division at a wavelength of 1550 nm manufactured in the CW-5000 workstation. A fibre-coupled external cavity tunable semiconductor laser (TSL-210, Santec) with a maximal output power equal to 20 mW was used. The spectrum line width of the laser is fairly narrow - typically equal to 1 MHz. The system was working during the coherence control function switched on, so the spectrum line width was in the range of 1–500 MHz according to the datasheet provided by the producer [43]. The wavelength of the laser source was set to 1550 nm. The TSL-210 ensures a wavelength tuning accuracy of 0.1 nm. The reference and sensing arms lengths were aligned so that the light coherence path was much greater than the difference in the length of the interferometer optical paths. The path difference was set to less than a few centimetres, which was related to the splicing process. The reference arm was shielded from external disturbances by a special attenuating material that covered the optical fibre. To control the vibration source obtained by the conventional speaker, a signal generator (DG4062, Rigol Technologies) was connected. The output signal was detected by a photodetector (PDA10CS-EC, Thorlabs), then converted to an electric signal and analysed on an oscilloscope (DSOX3012A, Keysight Technologies) using a fast Fourier transform (FFT) to accurately evaluate the harmonic frequencies of a given signal. The signal modulation was in the range from 1 Hz to 10 kHz with with a peak-to-peak voltage amplitude of 5 V.

During the experiment, three different types of sensing arms were applied. Firstly, a standard SMF was used and mounted on a special 3D-printed frame to keep the fibre over the speaker. Secondly, the PM was connected in the same way as the arm from the SMF. Strongly birefringent optical fibres (with additional attenuation discrimination of the second primary mode) are necessary for interferometric applications where the polarization states of the interfering light beams transmitted by the reference and sensing arms must be consistent, and the polarization separation must be at a high level. Then, a single-mode TOF was used. A biconical tapper was prepared with an elongation of 25.72 ± 0.14 mm, a taper fibre waist region of 5.37 ± 0.41 μm characterised by optical losses of 0.34 ± 0.03 dB. Process of the optical fibre tapering guarantees direct access to the guided light beam in the form of an evanescent field in the taper waist area [44, 45].

Results

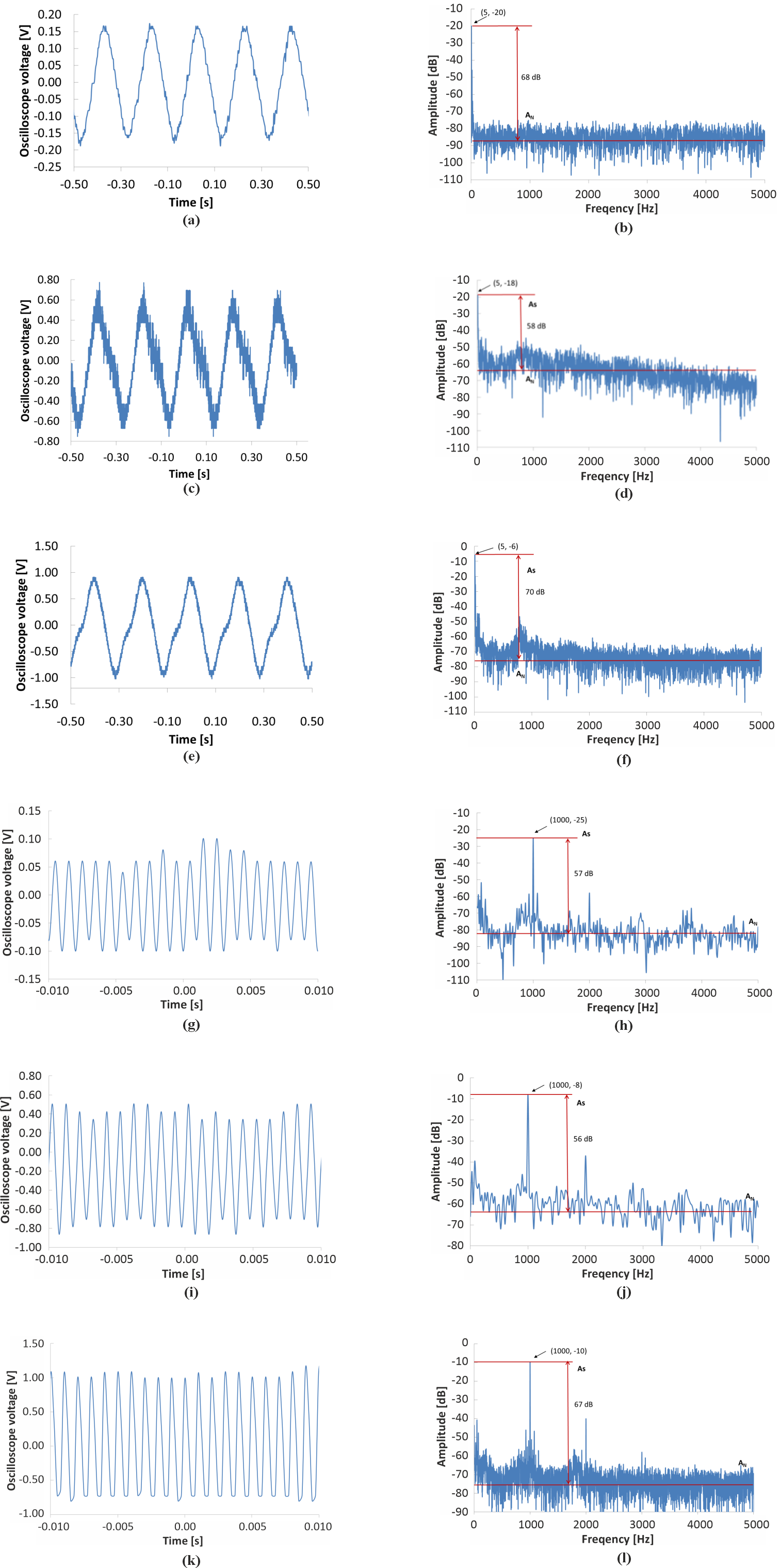
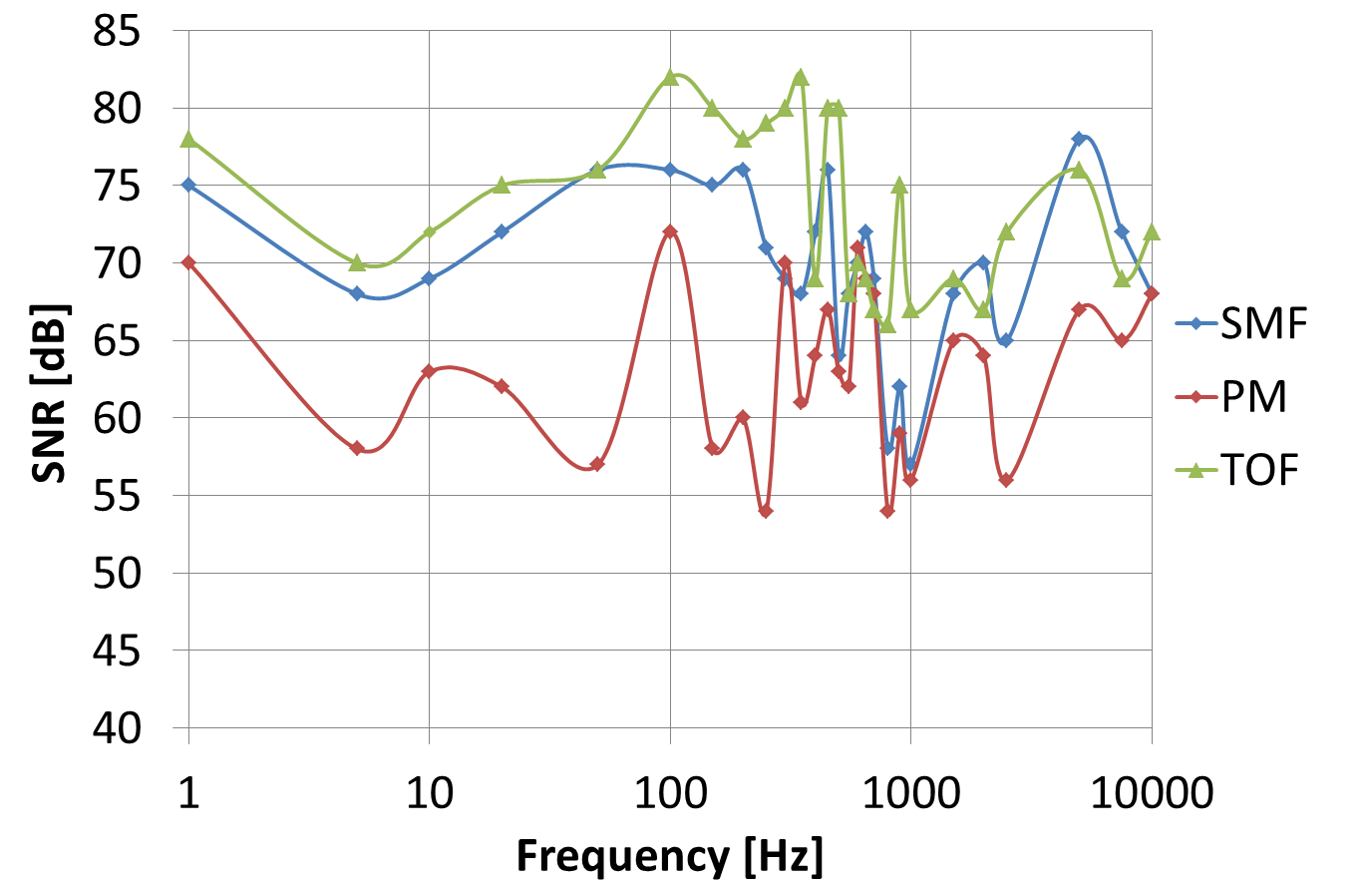
In order to clearly show the results, a time domain signal of the system at 5 and 1000 Hz was selected for analysis and presentation in Fig. 3. The presented graphs clearly show a relatively standard sinusoidal signal. Peak-to-peak voltage values of 5 Hz and 1000 Hz response signals were equal to 0.34 V and 0.2 V, 1.6 V and 1.3 V, as well as 2.0 V and 7.8 V for SMF, PM, and TOF sensing arm, respectively. It means that the highest value of the signal amplitude of the output response was obtained for the system with TOF. Moreover, the trace of the output curve for a system with TOF is the least disturbed. The signal for a system with PM is the most disturbed on the falling slopes, especially in the case of 5 Hz presented in Fig. 3(c). As it can be seen in Fig. 3, the FFT indicates a harmonic composition of the output signals – the first one corresponds to the set frequency, and the next one is its multiplication. However, the peak frequency was consistent with the value of the speaker loading frequency, indicating that the system reflected the vibration signal well. The signal-to-noise ratio (SNR) has been determined as the difference between the amplitude intensity at the peak point in the frequency spectrum As and the average amplitude intensity of noise of the frequency spectrum AN. The values of SNR of the investigated systems in the range from 1 Hz to 10 kHz are presented in Fig. 4. The highest SNR value was achieved by the system when using TOF in the sensing arm with an average value of 73.62 ± 4.73 dB. Despite the lower voltage value for the system with SMF in the sensing arm, this system is characterised by a higher value of SNR (average: 69.78 ± 4.01 dB) than the one with PM fibre (average: 63.07 ± 4.44 dB). This can be explained by noisier output signals. All the SNRs were higher than 54 dB in the entire frequency range, and the relatively higher SNR appeared at 100 Hz, 350 Hz, 450 Hz, and 500 Hz for TOF; 100 Hz, 450 Hz, and 5000 Hz for SMF; 100 Hz and 600 Hz for PM. The maximum SNR of the investigated TOF system at 100 Hz and 350 Hz reached 82 dB.

The signal-to-noise ratio (SNR) has been determined as the difference between the amplitude intensity at the peak point in the frequency spectrum As and the average amplitude intensity of noise of the frequency spectrum AN. The values of SNR of the investigated systems in the range from 1 Hz to 10 kHz are presented in Fig. 4. The highest SNR value was achieved by the system when using TOF in the sensing arm with an average value of 73.62 ± 4.73 dB. Despite the lower voltage value for the system with SMF in the sensing arm, this system is characterised by a higher value of SNR (average: 69.78 ± 4.01 dB) than the one with PM fibre (average: 63.07 ± 4.44 dB). This can be explained by noisier output signals. All the SNRs were higher than 54 dB in the entire frequency range, and the relatively higher SNR appeared at 100 Hz, 350 Hz, 450 Hz, and 500 Hz for TOF; 100 Hz, 450 Hz, and 5000 Hz for SMF; 100 Hz and 600 Hz for PM. The maximum SNR of the investigated TOF system at 100 Hz and 350 Hz reached 82 dB.

Conclusions

The optical fibre MZI configurations were investigated. The results show that all systems with different sensing arms detected signals at a given frequency. The constructed Mach-Zehnder set-up reflected all given frequency in the range from 1 Hz to 10 kHz. The highest value of SNR has been determined for the system with TOF as a sensing arm.

Moreover, the output signal time domain was the least disturbed for this system. This indicates that the TOF as a sensing arm in the MZI is the most advantageous. The paper emphasises the simplicity of the set-up structure and the detection capabilities based on the interferometric sensing using the commonly available devices in the laboratories.

The future research will be carried out using the optical fibre MZI with coated TOFs as the sensing arm to gain the frequency band of the sensor in the range from a few Hz to a few MHz. In order to construct the sensors with vibration localisation, a dual MZI will be manufactured. In the future set-up, a modulation element should be able to transform vibration up to MHz in order to examine the wider frequency band. The authors believe that it will provide valuable and applicable results.

Authors’ statement

This research was funded by Military University of Technology grant no. UGB 22-806.

References

1. ‌Mohd Ghazali, M. H. & Rahiman, W. Vibration analysis for machine monitoring and diagnosis: A systematic review. Shock. Vib. 2021, 9469318 (2021). https://doi.org/10.1155/2021/9469318

2. ‌Jafari, M. & Alipour, A. Methodologies to mitigate wind-induced vibration of tall buildings: A state-of-the-art review. J. Build. Eng. 33, 101582 (2021). https://doi.org/10.1016/j.jobe.2020.101582

3. ‌Hou, R. & Xia, Y. Review on the new development of vibration- based damage identification for civil engineering structures: 2010– 2019. J. Sound Vib. 491, 115741 (2021). https://doi.org/10.1016/j.jsv.2020.115741

4. ‌Agrawal, H. & Mishra, A. K. An innovative technique of simplified signature hole analysis for prediction of blast-induced ground vibration of multi-hole/production blast: an empirical analysis. Nat. Hazards 100, 111–132 (2020). https://doi.org/10.1007/s11069-019-03801-2

5. ‌Yan, Y., Li, T., Liu, J., Wang, W. & Su, Q. Monitoring and early warning method for a rockfall along railways based on vibration signal characteristics. Sci. Rep. 9, 6606 (2019). https://doi.org/10.1038/s41598-019-43146-1

6. ‌Feng, Z. & Yufeng, Z. Research Progress of Mechanical Vibration Sensors. in 2020 3rd World Conference on Mechanical Engineering and Intelligent Manufacturing (WCMEIM) 412–416 (IEEE, 2020). https://doi.org/10.1109/WCMEIM52463.2020.00093

7. ‌Wang, Y. et al. A comprehensive study of optical fiber acoustic sensing. IEEE Access 7, 85821–85837 (2019). https://doi.org/10.1109/Access.2019.2924736

8. ‌Liu, X. et al. Distributed fiber-optic sensors for vibration detection.Sensors 16, 1164 (2016). https://doi.org/10.3390/S16081164

9. Varanis, M., Silva, A., Mereles, A. & Pederiva, R. MEMS accelerometers for mechanical vibrations analysis: A comprehensive review with applications. J. Braz. Soc. Mech. Sci. 40, 527 (2018). https://doi.org/10.1007/s40430-018-1445-5

10. ‌Perrone, G. & Vallan, A. A low-cost optical sensor for noncontact vibration measurements. IEEE Trans. Instrum. Meas. 58, 1650– 1656 (2009). https://doi.org/10.1109/tim.2008.2009144

11. ‌Castrellon-Uribe, J. Optical Fiber Sensors: An Overview. in Fiber Optic Sensors (eds. Yasin, M., Harun, S. W. & Arof, H.) 1–28 (InTech, 2012). https://doi.org/10.5772/28529

12. ‌Bado, M. F. & Casas, J. R. A review of recent distributed optical fiber sensors applications for civil engineering structural health moni- toring. Sensors 21, 1818 (2021). https://doi.org/10.3390/s21051818

13. ‌Liaw, S. Introductory Chapter: An Overview the Methodologies and Applications of Fiber Optic Sensing. in Fiber Optic Sensing - Principle, Measurement and Applications (ed. Liaw, S.-K.) ch. 1 (IntechOpen, 2019). https://doi.org/10.5772/intechopen.86525

14. ‌Webb, D. J. Optical-fiber sensors: An overview. MRS Bull. 27, 365– 369 (2002). https://doi.org/10.1557/mrs2002.121

15. ‌Méndez, A. & Csipkes, A. Overview of Fiber Optic Sensors for NDT Applications. in Nondestructive Testing of Materials and Structures (eds. Güneş, O. & Akkaya, Y.) 179–184 (Springer, 2013). https://doi.org/10.1007/978-94-007-0723-8_26

16. ‌Bang, H.-J., Jun, S.-M. & Kim, Ch.-G. Stabilized interrogation and multiplexing techniques for fibre Bragg grating vibration sensors. Meas. Sci. Technol. 16, 813 (2005). https://doi.org/10.1088/0957-0233/16/3/024

17. Liang, T.-Ch. & Lin, Y.-L. Ground vibrations detection with fiber optic sensor. Opt. Commun. 285, 2363–2367 (2012). https://doi.org/10.1016/j.optcom.2012.01.037

18. Lu, L., Cao, Z., Dai, J., Xu, F. & Yu, B. Self-mixing signal in er3+−yb3+ codoped distributed bragg reflector fiber laser for remote sensing applications up to 20 km. IEEE Photon. Technol. Lett. 24, 392–394 (2012). https://doi.org/10.1109/LPT.2011.2179922

19. ‌Lu, L., Yang, J., Zhao, Y., Du, Z. & Yu, B. Self-mixing interference in an all-fiberized configuration Er3+–Yb3+ codoped distributed Bragg reflector laser for vibration measurement. Curr. Appl. Phys. 12, 659–662 (2012). https://doi.org/10.1016/j.cap.2011.09.018

20. Wang, C. et al. Quasi-distributed fiber sensor based on Fresnel- reflection-enhanced Incomplete-POTDR system. Proc. SPIE 9634, 96347F (2015). https://doi.org/10.1117/12.2194481

21. ‌Muanenda, Y., Oton, C. J., Faralli, S. & Di Pasquale, F. A cost- effective distributed acoustic sensor using a commercial off-the- shelf DFB laser and direct detection phase-OTDR. IEEE Photon. J. 8, 1–10 (2016). https://doi.org/10.1109/JPHOT.2015.2508427

22. ‌Ren, M., Lu, P., Chen, L. & Bao, X. Theoretical and experimental analysis of Φ-OTDR based on polarization diversity detection. IEEE Photon. Technol. Lett. 28, 697–700 (2015). https://doi.org/10.1109/LPT.2015.2504968

23. ‌Zhang, Q., Zhu, T., Hou, Y. & Chiang, K. S. All-fiber vibration sensor based on a Fabry Perot interferometer and a microstructure beam, J. Opt. Soc. Am. B 30, 1211–1215 (2013). https://doi.org/10.1364/JOSAB.30.001211

24. ‌Sathitanon, N. & Pullteap, S. A fiber optic interferometric sensor for dynamic measurement. Proc. World Acad. Sci. Eng. Technol. (PWASET) 26, 526–529 (2007).

25. ‌Giuliani, G., Norgia, M., Donati, S. & Bosch, T. Laser diode self- mixing technique for sensing applications. J. Opt. 4, S283 (2002). https://doi.org/10.1088/1464-4258/4/6/371

26. ‌Castellini, P., Martarelli, M. & Tomasini, E. Laser Doppler vibrometry: development of advanced solutions answering to technology’s need. Mech. Syst. Signal Process. 20, 1265–1285 (2006). https://doi.org/10.1016/j.ymssp.2005.11.015

27. ‌Chijioke, A. & Lawall, J. Laser Doppler vibrometer employing active frequency feedback. App. Opt. 47, 4952–4958 (2008). https://doi.org/10.1364/AO.47.004952

28. ‌Antunes, P. et al. Optical fiber accelerometer system for structural dynamic monitoring. IEEE Sens. J. 9, 1347–1354 (2009). https://doi.org/10.1109/JSEN.2009.2026548

29. ‌Liu, Q. P. et al. Novel fiber Bragg grating accelerometer based on diaphragm. IEEE Sens. J. 12, 3000–3004 (2012). https://doi.org/10.1109/JSEN.2012.2201464

30. ‌Guo, F. et al. High-sensitivity, high-frequency extrinsic Fabry–Perot interferometric fiber-tip sensor based on a thin silver diaphragm. Opt. Lett. 37, 1505–1507 (2012). https://doi.org/10.1364/OL.37.001505

31. ‌Wang, S. et al. An infrasound sensor based on extrinsic fiber-optic Fabry–Perot interferometer structure. IEEE Photon. Technol. Lett. 28, 1264–1267 (2016). https://doi.org/10.1109/LPT.2016.2538318

32. ‌Xie, S., Zhang, M., Li, Y. & Liao, Y. The influence of fiber inhomogeneity on the positioning accuracy of distributed fiber vibration sensor. Proc. SPIE 8561, 85610O (2012). https://doi.org/10.1117/12.999841

33. Tu, D., Xie, S., Jiang, Z. & Zhang, M. Ultra long distance distributed fiber-optic system for intrusion detection. Proc. SPIE 8561, 85611W (2012). https://doi.org/10.1117/12.2001292

34. Rao, Y. et al. Long-distance fiber-optic Φ-OTDR intrusion sensing system. Proc. SPIE 7503, 75031O (2009). https://doi.org/10.1117/12.835324

35. ‌Sun, Z., Xu, Y., Yu, W., Zhang, G. & Fang, W. Optical fiber distributed vibration sensor based on dual Mach-Zehnder interferometer using an improved phase generated carrier algorithm. Infrared Phys. Technol. 127, 104440 (2022). https://doi.org/10.1016/j.infrared.2022.104440

36. ‌Udd, E. A personal tour of the fiber optic Sagnac interferometer.Proc. SPIE 7316, 73160R (2009). https://doi.org/10.1117/12.819207

37. ‌Chen, Q. et al. A distributed fiber vibration sensor utilizing dispersion induced walk-off effect in a unidirectional Mach-Zehnder interferometer. Opt. Express 22, 2167–2173 (2014). https://doi.org/10.1364/OE.22.002167

38. ‌Zhao, Y., Xia, F., Chen, M. & Lv, R. Optical fiber low-frequency vibration sensor based on butterfly-shape Mach-Zehnder interferometer. Sens. Actuator. A Phys. 273, 107–112 (2018). https://doi.org/10.1016/j.sna.2018.01.051

39. ‌Tsuda, H., Koo, J.-H. & Kishi, T. Detection of simulated acoustic emission with Michelson interferometric fiber-optic sensors.J. Mater. Sci. Lett. 20, 55–56 (2001). https://doi.org/10.1023/A:1006714815182

40. ‌He, Q. et al. All fiber distributed vibration sensing using modulated time-difference pulses. IEEE Photon. Technol. Lett. 25, 1955–1957 (2013). https://doi.org/10.1109/LPT.2013.2276124

41. ‌Rao, Y. J. & Jackson, D. A. Principles of Fiber-Optic Interfero- metry. in Optical Fiber Sensor Technology: Fundamentals (eds. Grattan, K. T. V. & Meggitt, B. T.) 167–192 (Springer, 2000).

42. ‌Culshaw, B. & Dakin, J. (eds.) Fiber-Optic Gyroscope. in Optical Fiber Sensors, Vol. 2: Systems and Applications. (Artech House, Boston London, 1989).

43. (accessed: 12/16/2023).http://www.photonics.byu.edu/santec.parts/TSL-210.pdf

44. ‌Stasiewicz, K. A., Krajewski, R., Jaroszewicz, L. R., Kujawińska, M. & Świłło, R. Influence of the tapering process on optical fiber refractive index distribution changes along the structure. Opto- Electron. Rev. 18, 102–109 (2010). https://doi.org/10.2478/s11772-009-0030-y

45. ‌Stasiewicz, K. A. & Musiał, J. E. Threshold temperature optical fibre sensors. Opt. Fiber Technol. 32, 111–118 (2016). https://doi.org/10.1016/j.yofte.2016.10.009